1. Khái niệm ma trận nghịch đảo:
1.1 Định nghĩa 1:
Ma trận vuông cấp n I được gọi là ma trận đơn vị nếu A.I = I.A = A, với mọi ma trận vuông A cấp n
Ta thấy rằng ma trận đơn vị tồn tại. Thực sự, ma trận thỏa mãn điều kiện trên có dạng như sau:
Ngoài ra, ma trận đơn vị là duy nhất. Thật vậy, giả sử có hai ma trận đơn vị I và I’. Ta có:
Vì I là ma trận đơn vị nên I.I’ = I’.I = I’
và I’ là ma trận đơn vị nên I’.I = I.I’ = I
Do đó: I = I’
1.2 Định nghĩa 2:
Cho A là một ma trận vuông cấp n trên K. Ta nói A là ma trận khả nghịch nếu tồn tại một ma trận B vuông cấp n trên K sao cho: A.B = B.A = In . B khi đó được gọi là ma trận nghịch đảo của ma trận A, ký hiệu A-1.
Thật vậy, ta có: A.A-1 = A-1.A = In
1.3 Nhận xét:
1. Ma trận nghịch đảo là duy nhất, vì giả sử tồn tại ma trận C vuông cấp n cũng là ma trận nghịch đảo của A. Ta có: A.C = C.A = In , thì: B = B.In = B(A.C) = (B.A).C = In.C = C
2. Hiển nhiên: (A-1)-1= A, nghĩa là A lại là ma trận nghịch đảo của A-1
3. Trong giáo trình này, ta chỉ xét sự khả nghịch của ma trận vuông. Tuy nhiên, hiện nay, có nhiều giáo trình nước ngoài đã đề cập đến khái niệm khả nghịch của ma trận bất kỳ.
Thật vậy, cho A là ma trận cấp m x n trên trường số K. Khi đó, ta nói A là ma trận khả nghịch bên trái nếu tồn tại ma trận L cấp n x m sao cho: L.A = In; A là ma trận khả nghịch bên phải nếu tồn tại ma trận R cấp n x m sao cho: A.R = Im. Và khi đó, dĩ nhiên A khả nghịch nếu A khả nghịch bên trái và khả nghịch bên phải.
4. Ma trận đơn vị là khả nghịch, Ma trận không không khả nghịch.
5. Tập hợp các ma trận vuông cấp n trên K khả nghịch, được ký hiệu là GLn(K).
1.4 Các ví dụ:
Xét các ma trận vuông thực, cấp 2 sau đây:
Ta có: A.B = B.A = I2. Do đó: A, B là khả nghịch và A là nghịch đảo của B; B là nghịch đảo của A
Ma trận C không khả nghịch vì với mọi ma trận vuông cấp 2 ta đều có:
Nhận xét: Ma trận có ít nhất 1 dòng không (hoặc cột không) đều không khả nghịch.
2. Tính chất:
1. Nếu A, B là khả nghịch thì ma trận tích AB là khả nghịch và (AB)-1= B-1. A-1
2. Nếu A khả nghịch thì ATkhả nghịch và (AT)-1= (A-1)T
(Bạn hãy chứng minh kết quả trên nhé)
3. Mối quan hệ giữa ma trận khả nghịch và ma trận sơ cấp:
3.1 Ma trận sơ cấp: Ma trận E vuông cấp n trên K (n ≥ 2) được gọi là ma trận sơ cấp dòng (cột) nếu E thu được từ ma trận đơn vị In bằng duy nhất 1 phép biến đổi sơ cấp dòng (cột). Các ma trận sơ cấp dòng hay cột gọi chung là ma trận sơ cấp.
3.2 Tính chất: Tất cả các ma trận sơ cấp dòng (hay cột) đều khả nghịch và nghịch đảo của chúng lại là một ma trận sơ cấp dòng.
Ta có thể kiểm tra trực tiếp kết quả trên bằng thực nghiệm:
Ma trận sơ cấp dạng 1: nhân dòng của ma trận đơn vị với α ≠ 0
Ma trận sơ cấp dạng 2: cộng hàng i đã nhân với λ vào hàng j
Ma trận sơ cấp dạng 3: đổi chỗ hàng i và hàng j
3.3 Định lý:
Cho A là ma trận vuông cấp n trên K (n ≥ 2). Khi đó, các khẳng định sau đây là tương đương:
1. A khả nghịch
2. In thu được từ A qua một số hữu hạn các phép biến đổi sơ cấp dòng (cột)
3. A là tích của một số hữu hạn các ma trận sơ cấp
(Bạn đọc có thể tham khảo chứng minh định lý này trong các giáo trình về Đại số tuyến tính)
3.4 Hệ quả:
Cho A là ma trận vuông cấp n trên K (n ≥ 2). Khi đó, các khẳng định sau đây là tương đương:
1. A khả nghịch khi và chỉ khi dạng bậc thang của A là In
2. Nếu A khả nghịch thì In thu được từ A qua một số hữu hạn các phép biến đổi sơ cấp dòng (cột); và ngược lại, chuỗi các phép biến đổi sơ cấp dòng (cột) đó biến In thành nghịch đảo của ma trận A.
4. Thuật toán Gauss-Jordan tìm ma trận nghịch đảo bằng phép biến đổi sơ cấp:
Chúng ta sử dụng thuật toán Gauss-Jordan để tìm ma trận nghịch đảo (nếu có) của ma trận A vuông cấp n trên K. Thuật toán này được xây dựng dựa trên kết quả thứ 2 của hệ quả 3.4. Chúng ta thực hiện các bước sau:
Bước 1: Lập ma trận n hàng, 2n cột bằng cách ghép thêm ma trận đơn vị cấp n I vào bên phải ma trận A
Bước 2: Sử dụng các phép biến đổi sơ cấp dòng để biến [A|I] thành dạng [A’ | B], trong đó A’ là một ma trận bậc thang chính tắc.
– Nếu A’ = In thì A khả nghịch và A-1 = B
– Nếu A’ ≠ In thì A không khả nghịch. Điều này nghĩa là, trong quá trình biến đổi, nếu A’ có ít nhất 1 hàng không, ta ngay lập tức kết luận A không khả nghịch (không cần đưa A’ về dạng chính tắc) và kết thúc thuật toán.
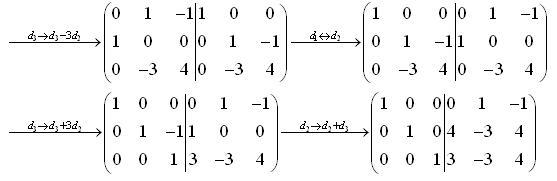
Ví dụ minh họa: Sử dụng thuật toán Gauss-Jordan để tìm ma trận nghịch đảo của:
Từ đó suy ra
Giải:
Vì vậy, ta có: A khả nghịch và:
Từ đó, có: . Do đó: